1. 백페이스 컬링
백페이스 컬링은 그리기 단계에서 화면상 보이지 않는 불필요한 폴리곤을 잘라내 렌더링을 하는 기법중 하나입니다.
컬링에는 백페이스 컬링, 오클루전 컬링, 프러스텀 컬링이 있습니다.
오클루전 컬링(Occlusion Culling)은 다른 오브젝트에 가려 카메라에 보이지 않는 오브젝트의 렌더링을 비활성화 하는 기법입니다.
프러스텀 컬링(View Frustum Culling)은 절두체 컬링이라고도 합니다. 해당 컬링은 실제로 카메라의 시야 범위에 포함되는 것들만 렌더링하고 나머지는 렌더링을 비활성화하는 기법입니다.
그럼 백페이스 컬링은 어떤 걸까요?
백페이스 컬링은 카메라에서 보이지 않는 뒷면의 폴리곤을 렌더링하지 않는 기법입니다.
일단 백페이스 컬링을 위해서는 그리기 순서가 필요합니다.
DirectX를 해보신 분을 알겠지만 DirectX에서 사각형을 그릴때 그리기 순서
즉 그려질 버텍스들의 인덱스 순서를 잘 맞춰줘야 원하는데로 그려집니다.
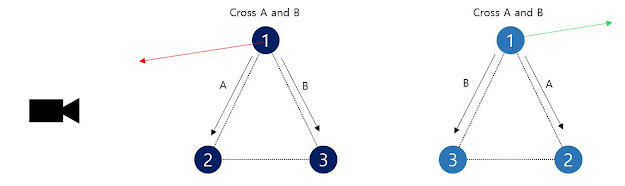
위와 같이 생긴 폴리곤을 그린다고 가정해보면 왼쪽 폴리곤은 반시계방향으로
오른쪽 삼각형은 시계 방향으로 돌아가며 그려집니다.
즉 왼쪽 폴리곤은 그려지고 오른쪽 폴리곤은 컬링 됩니다.
그럼 이걸 어떻게 컴퓨터에서 인지하고 컬링을 해줄까요?
위의 정보는 두 벡터 값으로 표현할 수 있습니다.
그리고 두 벡터 값을 외적하면 해당 축과 직교하는 벡터가 나오는데
이 벡터가 카메라 방향을 향한다면 그려주고 반대라면 컬링합니다.
이제 방향을 향하고 있는지 아닌지는 내적을 이용하면 간단하게 구할수 있습니다.
사용하는 코드에서는 오른손 좌표계를 사용하기 때문에 화면에 그릴려면 (0,0,-1)과 내적하여 양수의 값이 나온다면 컬링합니다.
반대로 (0,0,1)로 내적하면 결과 값이 양수라면 그려주기만 하면됩니다.
왼쪽: 백페이스 컬링 미적용, 오른쪽: 백페이스 컬링 적용
2. 원근 투영
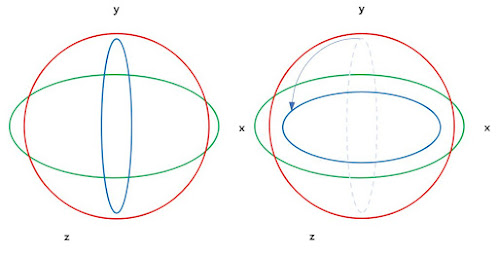
원근 투영 행렬을 유도하기 전에 카메라가 렌더링할 영역을 보면
아래와 같은 모양의 절두체가 나올 겁니다.
절두체는 6개의 평면으로 구성됩니다.
해당 공간을 X 축에서 바라보도록 단순화하여 정리해보려 합니다.
위의 영역에서 카메라상의 영역이 모니터에 그려진다고 볼 수 있습니다.
그려지는 상의 위치 즉 스크린의 위치는 시야각에 따라 정해지며
카메라로부터 상이 맺히는 지점까지의 거리를 초점 거리라고 합니다.
초점 거리는 화면 높이의 절반 값과 시야각 이용하여 구할 수 있습니다.
화면의 해상도가 1280 x 720 이라고 한다면 360이 화면의 높이 값입니다.
하지만 모니터의 화면 해상도는 모니터에 따라 제각각입니다.
그래서 좌표를 정규화할 필요가 있는데 이를 NDC(Normalized Device Coordinate) 좌표라고 합니다.
NDC 좌표는 아래 이미지처럼 가로, 세로의 크기가 2인 사각형으로 이루집니다.
그럼 이제 NDC로 화면 크기를 정규화했으니 절반의 높이는 1이 되므로 초점 거리는 간단하게 구할 수 있습니다.
이제 절두체 안의 한 점을 그린다고 가정하고 화면에 투영한 위치를 구해보겠습니다.
일단 뷰 좌표계를 통해 변환된 점의 위치를

라고 하고
화면에 투영된 위치 즉 NDC 좌표 위치를

라고 봤을때

의 y 좌표값은

이기 때문에
의 결과를 가집니다.
그리고

의 x 좌표값은 아래와 같이 구할수 있을 겁니다.
이제 x y 좌표를 구했기 때문에 화면의 해상도를 곱해 물체의 최종 위치만 구해주면 됩니다.
하지만 우리가 화면으로 투영하려는 것은 3D 좌표상의 물체입니다.
이 상태로 그려준다면 z 의 값 즉 깊이 값이 없어 항상 나중에 그린 물체가 항상 보이게 될 것입니다.
그럼 뒤에 있는 물체가 앞에 그려지고 섞이거나 이상하게 그려질 겁니다.
그래서 NDC 좌표계는 z 축까지 포함해 3차원으로 구성됩니다.
동차 좌표계의 w 성분을 나누어 데카르트 좌표계로 만드는 과정을 보면 아래와 같이 표현할 수 있을 겁니다.
그리고 NDC의 x와 y의 값은 앞서 구했기 때문에 투영 행렬의 첫 두줄은 아래와 같이 볼 수 있다.
여기서 -z의 값은 공통 분모인데 이 값을 w'라고 한다면 각 값을 w'로 나누어 주면 데카르트 좌표계가 된다.
그리고 i j 의 값이 변경 된다고 NDC의 z 값에 영향을 주지는 않기 때문에 0으로 더 간략화시킬 수 있다.
이제 남은 k와 l의 값을 구해야 한다.
z의 값이 근평면인 경우를 보면 z의 값이 근평면일때 NDC의 z 값은 -1이 됩니다.
이를 적용한 행렬의 결과 값은 다음과 같이 나와야 한다.
n = near
즉 다음과 같은 식을 유도할 수 있다.

z가 원평면인 경우를 보면 NDC의 z 값은 1입니다.
f = far
이건

로 유도 해볼 수 있다. 그리고
두 식을 연립 방정식으로 풀면 다음과 같이 나옵니다.
이 식을 이용해 최종 행렬을 만들면
위와 같은 행렬이 만들어 집니다.
이 행렬을 앞서 포스팅했던 카메라의 행렬에 곱해주고 모델의 매트릭스에 곱해주기만 하면 됩니다.
float a = (float)InScreenSizeY / (float)InScreenSizeX;
float d = 1.0f / tanf(Math::Deg2Rad(FOV) * 0.5f); // 초점 거리
float nf = 1.0f / (NearZ - FarZ);
Vector4 xView = Vector4(a * d, 0, 0, 0.0f);
Vector4 yView = Vector4(0, d, 0, 0.0f);
Vector4 zView = Vector4(0, 0, (NearZ + FarZ) * nf, -1.0f);
Vector4 wView = Vector4(0, 0, (2 * NearZ * FarZ) * nf, 0.0f);
return Matrix4x4(xView, yView, zView, wView);
추가로 시야각 즉 FOV 값은 시야각이 커질수록 tan값이 증가하고 초점 거리는 그에 반비례하여 줄어듭니다. 그렇기 때문에 시야각이 좁아지면 물체가 크게 보이고 커지면 물체가 작게 보입니다.
아래와 같이 그림으로 봐도 넓은 각에 비해 각이 좁으면 물체가 크게 보일 것이다 라는 것을 알 수 있습니다.
처음에는 행렬과 계산하는게 마구 나와서당황했지만 결국에는 비율로 무언가를 한다!
라는 거에 지나지 않아서 직접 정리하면서 생각해보니 어려운 개념은 아닌것 같습니다.









댓글
댓글 쓰기