이번에는 과제로 나온 브레젠험 직선 알고리즘에 대한 글입니다.
1. 브레젠험 직선 알고리즘이란?
컴퓨터에서 계산이 느린 실수 연산을 사용하지 않고 직선을 그리기 위해
브레젠험(Bresenham's) 이라는 분이 만든 알고리즘입니다.
2. 기본 원리
일단 선을 만들려면 두 점이 필요합니다.
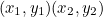
의 좌표로 이루어진 두 점이 있다고 보면 점에 대한 직선의 방정식은
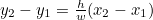
으로 정의할 수 있습니다. 좀더 단순하게 바꾸면
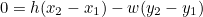
으로도 정의할 수 있습니다.
위와 같이 무언가 수식을 정리하긴 했습니다.
이제 저걸 어떻게 사용하는지가 핵심이라고 봅니다.
기본적으로 스크린 좌표는 정수형입니다.
브레젠험 알고리즘은 평면을 아래와 같이 8분 면으로 나누어 그립니다.
저렇게 나누어진 분면 위에서 점이 한 칸 더 가서 그려지냐 아니면 그대로 그려지냐 판별하는 것이 핵심입니다.
 3. 1분면에 대해 선 그리기
3. 1분면에 대해 선 그리기
브레젠험 알고리즘은 기울기가 0과 1사이일 때를 가정해 정리가 됩니다.
1분 면에서 아래와 p1과 p2를 이어주는 선을 그린다고 가정을 해봅시다.

사각형 하나는 1픽셀입니다.
그림을 보면 그리려 하는 선이 초록색으로 강조해놓은 팩셀 모두를 지나갑니다.
이때 위의 픽셀과 아래의 픽셀 중 하나를 선택해 그려줘야 합니다.
여기서 기울기는 항상 0과 1사이라서 x 값은 항상 1씩 증가합니다.
y 축은 L1 보다 L2의 값이 작으면 y값을 1 증가시켜줍니다.

위의 사이 값을 아래의 좌표와 같다고 생각해봅시다.

위의 좌표 값을 대입한 값이 해당 지점의 값

을 대입했을 때의 실제 Y값 보다 작으면 해당점은 픽셀위치의 변동 없이 그려주고 반대의 경우에는 한칸 아래에 그려줍니다.
해당 지점의 값을 직선의 방정식에 대입해보겠습니다.

그리고 y의 값은
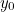
에서 0.5 증가했으니 아래와 같은 판별식을 만들수 있습니다.

하지만 나눗셈이라던지 0.5 실수를 더한다던지 아직 속도가 비교적 느린 부족한 부분이 있습니다.
양변에 w를 곱하고 조금더 간소화 시켜보겠습니다.
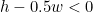
아직 실수 연산이 남아있네요. 그럼 변에 2를 곱해서 마무리를 짓겠습니다.
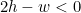
간단한 판별식이 나왔습니다.

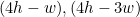
두번째 지점에 대한 판별식을 보겠습니다.
첫번째 점의 판별식
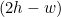
봅시다.
일정한 패턴이 있는 것을 확인 하수 있습니다.
이로서 모든 준비가 되었습니다.
이제 두 번째 픽셀의 y값을 정하기 위해 점화식
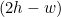
을 구합니다.
해당 지점의 판별식을 통해 y 값이 그대로 유지되면 다음 판별식은 2h를 더하고
y 값이 증가하면 다음 판별식은 2h-2w를 더한 값이 된다.
x의 값이 목표에 도달할 때까지 위의 과정을 반복하면 된다.
이로서 1분면에 선을 그릴수 있게 되었습니다!
int y = startPosition.Y;
int det = (2 * height) - width; // 점화식
for (int x = startPosition.X; x != endPosition.X; x += 1)
{
if (det < 0) //
{
det += 2 * height;
}
else
{
y += 1;
det += (2 * height - 2 * width);
}
SetPixel(ScreenPoint(x, y), InColor);
}
4. 나머지 분면
일단 2팔분면을 생각해보겠습니다.

1팔분면에서는 x의 값을 증가하고 y의 값을 판별했습니다.
하지만 2팔분면에서는 x의 값을 1식 증가시킬 수 없기 때문에
반대로 생각해야 합니다. 판별식은 같습니다. 단지 y를 증가하고 x의 위치를 판별하면 됩니다.
판별식은
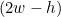
가 될 겁니다.
하나 더 생각해보겠습니다. 8분면을 생각하면 y의 값이 점점 줄어 들어야합니다.
나머지 분면도 이런식으로 생각해서 알고리즘을 사용하면 모든 분면에 선을 그릴수 있습니다.
5. 최종
// 넓이와 높이는 절대값으로 구해둠
int width = abs(endPosition.X - startPosition.X);
int height = abs(endPosition.Y - startPosition.Y);
int Yfactor = endPosition.Y < startPosition.Y ? -1 : 1;
int Xfactor = endPosition.X < startPosition.X ? -1 : 1;
// 넓이가 높이보다 큰경우는 1,4,5,8 분면
if (width > height)
{
int y = startPosition.Y;
int det = (2 * height) - width; // 점화식
for (int x = startPosition.X; x != endPosition.X; x += Xfactor)
{
if (det < 0) //판별
{
det += 2 * height;
}
else
{
y += Yfactor;
det += (2 * height - 2 * width);
}
SetPixel(ScreenPoint(x, y), InColor); // 점을 그려줌
}
}
else
{
int x = startPosition.X;
int det2 = (2 * width) - height; // 점화식
for (int y = startPosition.Y; y != endPosition.Y; y+= Yfactor)
{
if (det2 < 0)
{
det2 += 2 * width;
}
else
{
x += Xfactor;
det2 += (2 * width - 2 * height);
}
SetPixel(ScreenPoint(x, y), InColor);
}
}


댓글
댓글 쓰기