게임엔진프로그래밍 - 수학

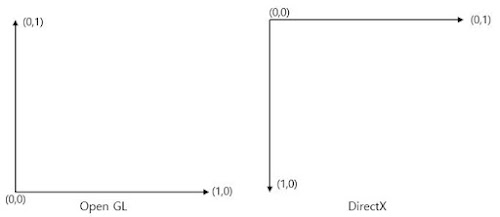
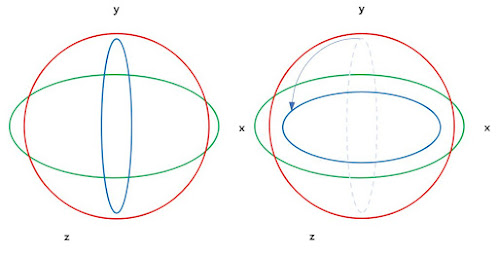
1. 브레젠험 직선 알고리즘 컴퓨터에서 계산이 느린 실수 연산을 사용하지 않고 직선을 그리기 위해 만들이진 알고리즘입니다. 평면을 아래와 같이 8분 면으로 나누어 직선을 그립니다. 링크: https://sulinep.blogspot.com/2020/05/bresenhams-line-algorithm.html 2. 엔진 기초 수학 여기서는 본격적으로 구현에 들어가기 전 기초 수학 지식을 쌓았습니다. 수학에서의 체는 대수적 구조의 하나로 덧셈, 뺄셈, 곱셈, 나눗셈의 사칙연산을 집합 안에서 소화할 수 있는 집합을 의미합니다. 체를 이루기 위한 조건과 체라는 개념을 알아보았습니다. 처음에 체 라는 개념이 뭔가 머릿속에서 애매했는데 이후 갈로이스 체에 대해 배운 후 조금 더 명확해졌습니다. 스칼라 는 벡터를 정의하기 위한 필수 요소이고 크기만 있고 방향이 없는 성분이다. 벡터는 크기와 방향을 포함하는 표현 도구이다. 겨기서 벡터의 기본 연산자들을 알아보았습니다. 선형성 은 직선처럼 똑바른 도형 또는 그와 비슷한 성질을 가진 대상이라는 뜻으로 함수의 경우 함수가 진행하는 모양이 직선이라는 의미로 사용된다. 선형성을 만족하려면 두 가지 조건을 만족해야 하는데 균질성과 첨가성이다. homogeneity (균질성): additivity (첨가성): 선형이라고 부르는 수식들은 중첩의 원리 가 적용된다는 특징이 있다. 이때 행렬과 선형 변환의 관계에 대하여도 알아보았었는데 선형 변환과 행렬은 1:1 대응된다. 기저 란 어떤 벡터 공간을 선형 생성하는 선형 독립인 벡터들이다. 각각의 원소들이 다시 벡터 공간을 생성할 수 있어야하고 일차 독립이어야 한다. 표준 기저 는 많은 기저들 중 성분 1개만이 1이고 나머지 성분이 모두 0인 표준 적인 벡터이다. 여기서 벡터 공간 R의 기저를 구성하는 원소의 개수가 해당 공간의 차원 이다. 행렬 은 열기반 행렬과 행기반 행렬 중 어떤 걸 사용하느냐에 따라 계산 방식이 달라진다. 여기서는 벡터의 크기, 회전, ...






댓글
댓글 쓰기