이번 글은 과제로 나온 갈로이스 체와 아핀 조합에 대한 글입니다.
1. 갈로이스 체 (Galois Field(GF2))
갈로이스 체는 0과 1로 구성된 가장 작은 유한체입니다.
앞서 체를 이루기 위해서는 사칙연산, 교환법칙... 등 여러가지 조건이 있었습니다.
갈로이스 체로 이들을 알아보려합니다.
1) 덧셈 연산
갈로이스 체의 덧셈 연산은 아래와 같습니다.
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 0
여기서 특이한 경우가 하나 있습니다. 1 + 1 = 0입니다(???)
보통 우리가 알고 있는 수학 계산을 한다면 분명 2가 나와야 합니다.
하지만 갈로이스 체는 0과 1로 이루어져 있고 이 두 개의 수로만 체의 조건이 만족되어야 합니다. 즉 2라는 수는 갈로이스 체에서 성립될 수 없습니다.
근데 왜 1이 아니고 0일까?
그래서 GF(3) 도 한번 살펴 보았습니다. GF(3)는 0,1,2로 이루어져 있는데
GF(3)에서 1+2=0, 2+2=1 이라는 결과가 나와 있었습니다.
확인해 보면 체 안에서 순환을 돈다는 것을 알 수 있었습니다.
덧셈에 대한 항등원 = 0
덧셈에 대한 역원 = 자신
덧셈의 결과를 보면 XOR 연산과 동일한 것을 볼수있다.
2) 곱셈 연산
곱샘 연산은 아래와 같습니다.
0 * 0 = 0
0 * 1 = 0
1 * 0 = 0
1 * 1 = 1
곱샘은 기존에 사용하던 계산 방식과 별 차이가 없습니다.
곱셈에 대한 항등원 = 1
곱셈에 대한 역원 = 0일때는 제외. 1이거나 혹은 자신
덧셈의 결과를 보면 AND 연산과 동일한 것을 볼수있다.
3) 결합, 교환 분배 법칙
결합 법칙: (0+1)+1 = 0+(1+1) (0*1)*1 = 0*(1*1)
교환 법칙: 0+1 = 1+0 0*1 = 1*0
분배 법칙: 1*(1+0) = (1*1)+(1*0)
세가지 경우 모두 만족한다.
4) 갈로이스 체로 만드는 벡터
갈로이스 체의 값들로 벡터를 만든다면 다음과 같이 나올 것입니다.
이 벡터들로 연산 또한 가능하다.
예를 들어 덧셈은

의 결과가 나올것이다.
곱셈은

이 될것이다.
행렬 연산도 가능하다.
2. 아핀과 컨벡스 (Affine, Convex)
1) 아핀조합
아핀 조합(Affine combination)은
아핀 공간에 속한 점
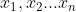
들이 주어졌을때

에서
상수 a의 값이 항상 1이어야만 한다.
이러한 결과가 만족되었을때, 두 점을 지나는 직선상의 모든 점들은 아핀 조합으로 표현할 수 있다.
위와 같이 아핀 조합에 대해 닫혀있는 집합을 Affine Set이라고 한다.
아핀 조합을 이용해 해당 집합의 여러 점을 구할 수 있을 것입니다.
2) 컨벡스 조합
일단 컨벡스를 직역하면 볼록이다.
컨벡스란 어떤 2개의 지점을 선으로 연결했을 때, 그 선을 이루는 요소들이 그 집합 안에 속해 있다면 그 집합을 Convex set(볼록 집합)이라고 한다.
컨벡스 조합은 위의 아핀 조합에서 모든 계수들이 0 이상이라는 조건이 추가로 붙는다.

의 조건과

이 만족해야한다.
3) 아핀 조합과 컨벡스 조합의 비교
유한개의 벡터
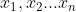
와 실수

에 대하여 선형결합으로 나타낼 수 있다는 것은 같다.
단 컨벡스는

이라는 조건이 추가로 붙는다.
임의의 원소
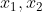
가 포함되어 있는 최소한의 Affine Set 과 Convex Set 을 구성해보면 다음과 같을 것이다.
4) 상수 값의 제약에 따른 선의 형태
위의 아핀 조합과 컨벡스 조합을 보면 앞에 붙는 상수의 조건에 따라 선의 모양이 달라진다.
이걸 이용하면 아래와 같이 나타낼 수 있을 것이다.
이것을 알기 전까지 유니티의 Ray가 Razer의 Ray인줄 알았다는 사실...
5) 컨벡스 도형의 특징
컨벡스 조합에 대해서 닫혀 있는 집합을 Convex Set이라고 한다.
이 집합에서 n개의 원소
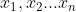
을 임의로 추출 했을때 해당 원소들의 컨벡스 조합도
해당 집합에 속하게 된다.
이를 그림으로 나타내면 다음과 같을 것이다.
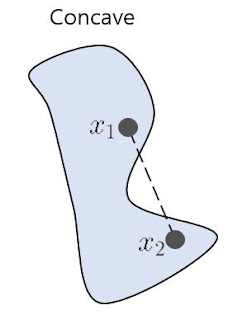
하지만 concave 도형 즉 오목한 도형은 어떨까
원소를 임의로 추출했을 때 컨벡스 조합이 해당 집합 안에 포함하지 않는다는 것을 알 수 있다.
3. 무게 중심 좌표(Barycentric Coordinate)
사실 무게 중심 좌표는 이해가 안되는 부분이 많았습니다.
수식이나 중심을 구하는 방법이나 이런건 보면 알겠지만
머리속으로 딱 이게 뭐다라는 감이 안잡힙니다.
그래도 인터넷이나 이곳 저곳에서 찾아본 내용이라도 간단하게 작성했습니다.
Barycentric Coordinate란 무게 중심 좌표입니다.
모양이 삼각형이라고 예를 들면
삼각형의 면적의 비율로도 생각할수 있습니다.
삼각형을 무게를 가지는 하나의 물체로 봤을 때 삼각형의 총 무게가 작용하는 작용점입니다.
물리적인 의미는 삼각형이 무게중심 위에 정확히 위치하면 삼각형이 기울거나 쓰러지지 않습니다.
무게 중심 좌표 도식화
 |
| 유니티상에서 좌표를 찍어 만든 모습 |
추가. 왜 3-Simplex는 사각형이 아니고 삼각뿔일까
n차원의 Simplex는 n+1개의 꼭짓점을 가진다.
그렇기 때문에 삼각뿔의 모양이 나온다.
즉 3차원 공간의 xzy의 좌표와 원점의 좌표를 이으면 삼각뿔이다.
3-Simplex는 위의 도식화 그림을 참고해도 될것 같습니다.







댓글
댓글 쓰기